How Do You Change The Frequency Of The Vibrator
Vibration and vibration isolation are both intimately continued with the miracle of resonance and unproblematic harmonic motion.
External forcefulness, either from a one-fourth dimension impulse or from a periodic forcefulness such every bit vibration, will cause the system to resonate as the spring alternately stores and imparts energy to the moving mass. A elementary example of harmonic movement is a mass connected to a flexible cantilevered beam. Effigy 1 below illustrates a simple mass on a cantilevered beam resonating nether the influence of an external force.
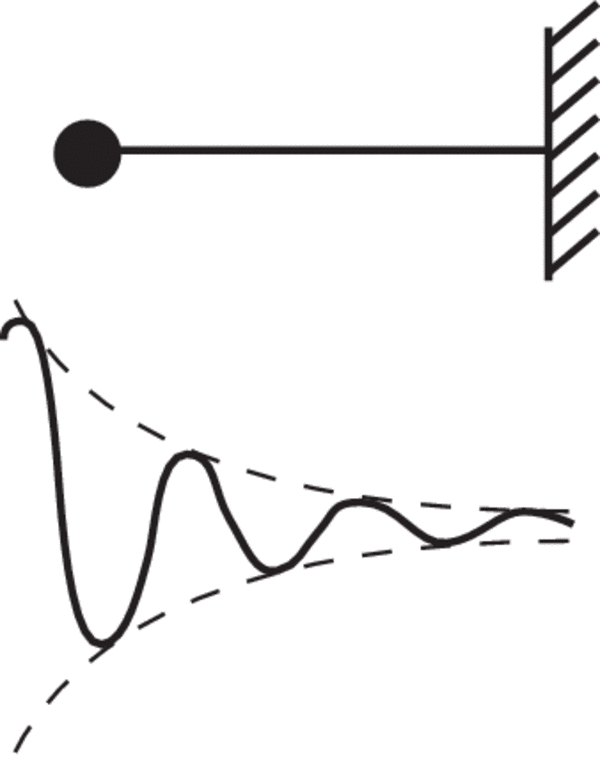
Figure ane. A simple mass on a cantilevered beam resonating under the influence of an external forcefulness.
The natural frequency, as the proper noun implies, is the frequency at which the organisation resonates. In the example of the mass and beam, the natural frequency is determined past two factors: the amount of mass, and the stiffness of the beam, which acts as a spring. A lower mass and/or a stiffer beam increase the natural frequency (see figure ii).
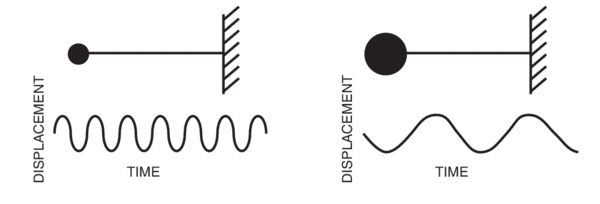
Figure 2. (Left) A lower mass increases natural frequency (left). A college mass lowers natural frequency (right)
A higher mass and/or a softer beam lower the natural frequency (see figure 3).
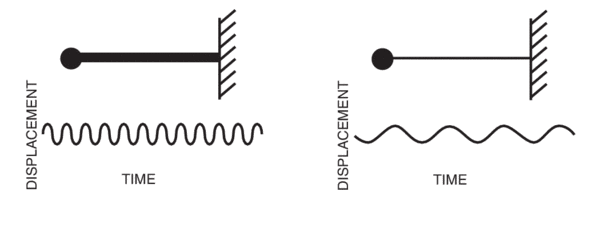
Effigy three. A stiffer leap increases natural frequency (left). A more than compliant ("softer") spring decreases natural frequency (right).
Some other elementary example of natural frequency is a tuning fork, which is designed to vibrate at a particular natural frequency. For example, a tuning fork for the musical annotation "A" vibrates at a frequency of 440 Hz. Just as the natural frequency of the cantilevered beam can be changed with a dissimilar spring rate or a change in the mass, the natural frequency of the tuning fork tin exist altered by adding or reducing mass of the two tines and/or by making the tines longer or shorter.
In the cantilevered beam and tuning fork models, we considered undamped systems in which there is no mechanism to misemploy mechanical energy. Without damping, these systems volition vibrate for quite a long period of time — at least several seconds — before coming to residuum.
Damping dissipates mechanical free energy from the organisation and attenuates vibrations more quickly. For example, when the tuning fork's tips are immersed in water, the vibrations are almost instantly attenuated. Similarly, when a finger touches the resonating mass-beam system lightly, this damping action besides quickly dissipates the vibrational energy.
The Simple Harmonic Oscillator consists of a rigid mass M connected to an ideal linear spring as shown in Figure four.
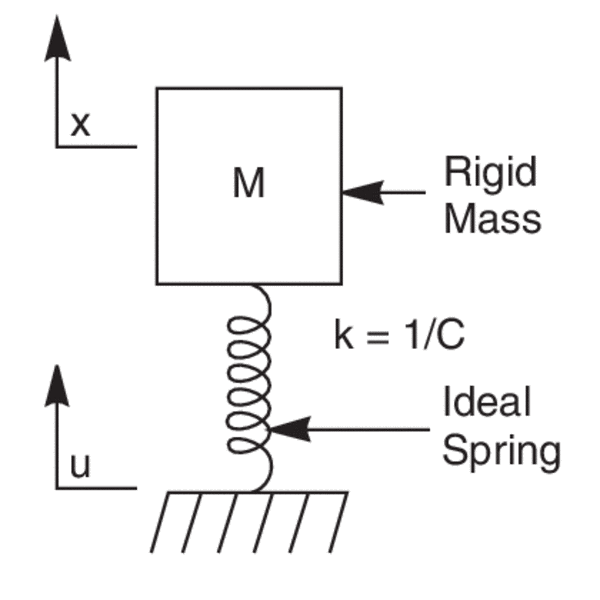
Effigy 4. A simple harmonic oscillator.
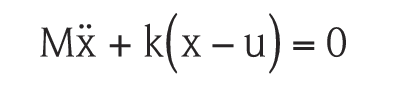
The spring has a static compliance C, such that the change in length of the leap Δx that occurs in response to a force F is: Δx = C F
Notation that the compliance C is the inverse of the spring stiffness (denoted by k) such that k = ane/C.
If the spring-mass organisation is driven by a sinusoidal displacement with frequency ω and peak amplitude |u| information technology will produce a sinusoidal displacement of the mass M with peak amplitude |x| at the aforementioned frequency ω. The steady-country ratio of the amplitude of the mass motion |x| to the spring finish motion |u| is called the transmissibility T and is given past:
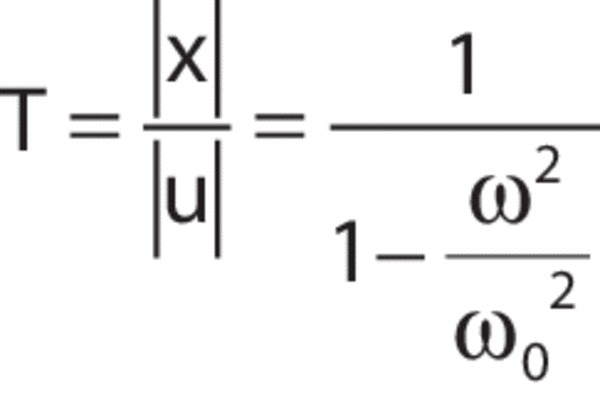
Where ω0 is the resonant, or natural frequency of the system given by:
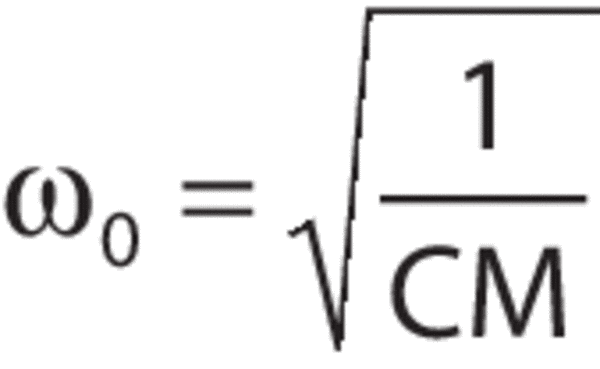
Note that the natural frequency of the system, ω0, is determined solely by the mass and the spring compliance. Information technology decreases for a larger mass or a more compliant (softer) spring. The transmissibility, T, of the organisation is plotted every bit a function of the ratio ω/ω0 (on a log-log plot in Effigy five.)
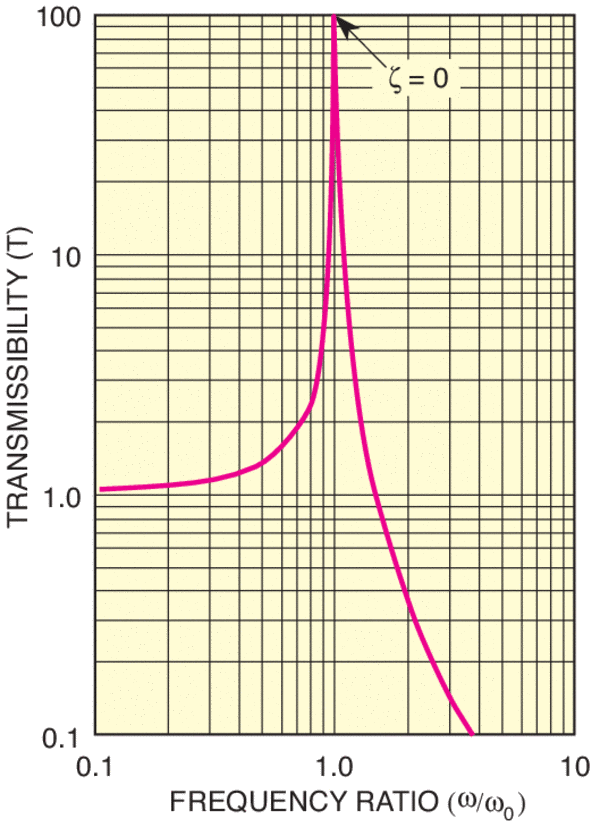
Figure v. Transmissibility of a Simple Harmonic Oscillator.
The three characteristic features of this system are:
- For ω « ω0, well below the resonance frequency, the transmissibility T = 1 and then the motility of the mass is the same as the motility at the other end of the bound.
- For ω ≈ ω0, near resonance, the motion of the leap finish is amplified, and the motion of the mass |x| is greater than that of |u|. For an undamped system, the move of the mass becomes theoretically infinite for ω = ω0.
- For ω » ω0, the resulting displacement |ten| decreases in proportion to 1/ω2. In this case, the displacement |u| applied to the system is not transmitted to the mass. In other words, the spring acts as an isolator.
In the first model, we considered an undamped system in which there is no mechanism to dissipate mechanical free energy from the mass-spring organisation. Damping refers to a mechanism that removes the mechanical energy from the organization—very often as heat. A damped Uncomplicated Harmonic Oscillator is shown schematically in Figure vi.
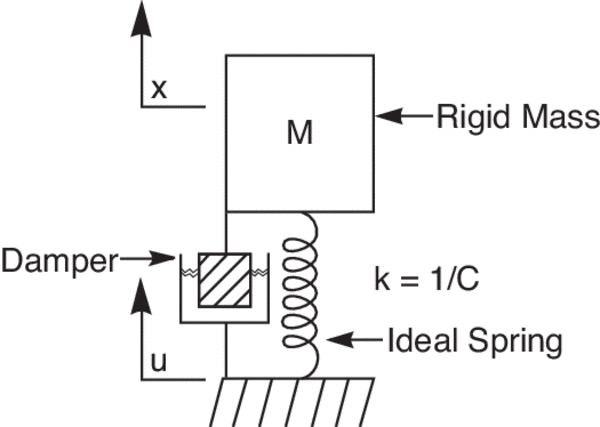
Effigy 6. A damped elementary harmonic oscillator.
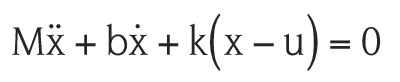
A rigidly connected damper is expressed mathematically past calculation a damping term proportional to the velocity of the mass and to the differential equation describing the move. For an external forcefulness that results in a displacement amplitude |u| of the end of the spring every bit in Model I, the transmissibility, T, of the damped system becomes:
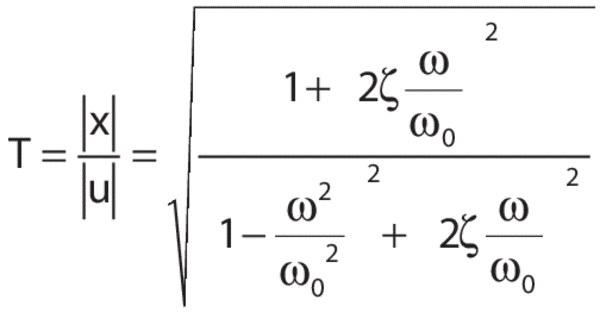
where ζ is a "damping" coefficient given by:
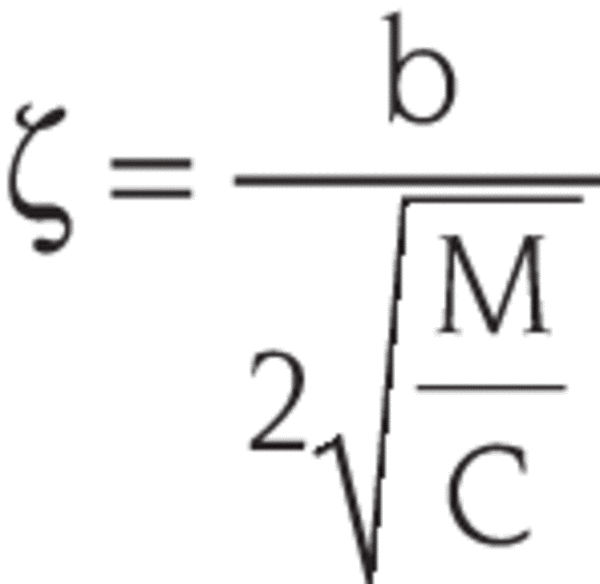
A plot of the transmissibility T is shown in Figure four for diverse values of the damping coefficient ζ. In the limit where ζ approaches zero, the curve becomes exactly the same every bit in Model I, that is, at that place is infinite amplification at the resonance frequency ω0. As the damping increases, the amplitude at resonance decreases. Nevertheless, the "coil-off" at college frequencies decreases (i.e. the transmissibility declines more slowly as damping increases). For ω/ω0 » ane/ζ, note that the motion of |x| is proportional to one/ω, equally compared to Model I where at high frequencies the motion of |ten| decreases as 1/ω2.
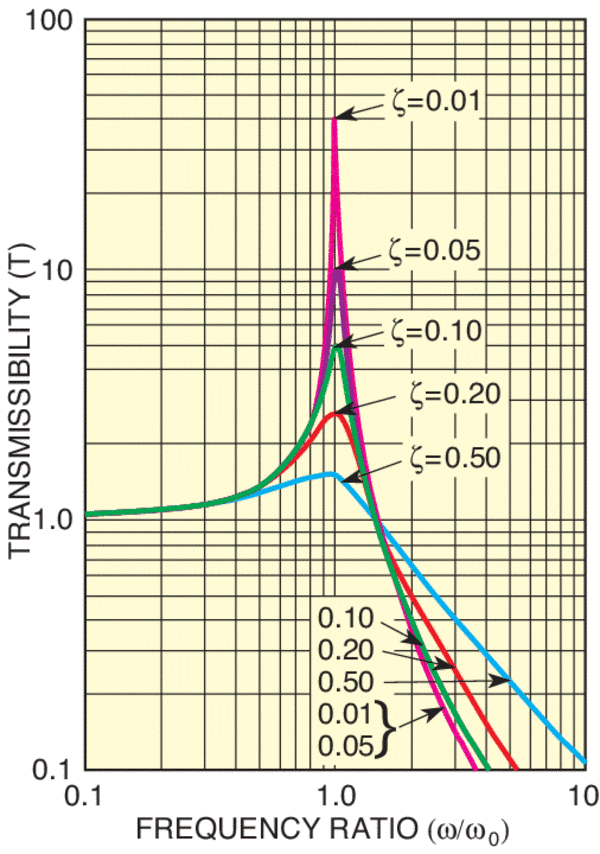
Figure 7. Transmissibility of a damped oscillator organisation with various values of the damping coefficient (ζ).
Source: https://www.newport.com/t/fundamentals-of-vibration
Posted by: pylantantless.blogspot.com


0 Response to "How Do You Change The Frequency Of The Vibrator"
Post a Comment